
In this short paper, we will try to follow the history of prime numbers since ancient times and use this opportunity to dive into and better understand the mathematician’s world. On a small scale, the appearance of prime numbers seems random, but on a large scale there appears to be a pattern, which is still not fully understood.
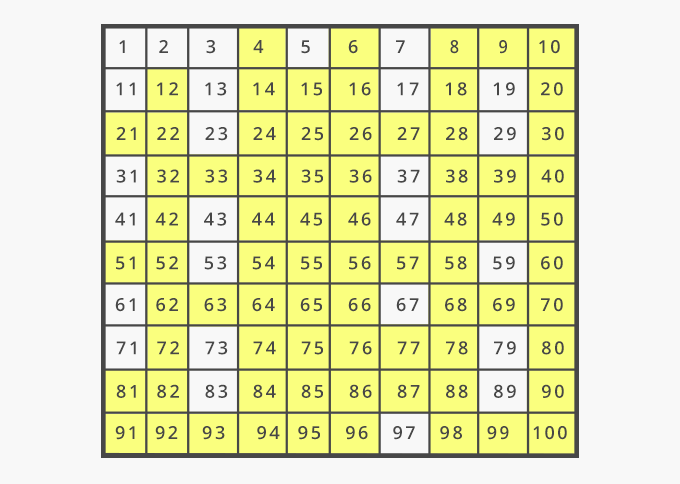
What are they? Why are the questions related to them so hard? One of the most interesting things about prime numbers is their distribution among the natural numbers. We explain what they are, why their study excites mathematicians and amateurs alike, and on the way we open a window to the mathematician’s world.įrom the beginning of human history, prime numbers aroused human curiosity.

The following are the prime factorizations of some common numbers.Prime numbers have attracted human attention from the early days of civilization. While these methods work for smaller numbers (and there are many other algorithms), there is no known algorithm for much larger numbers, and it can take a long period of time for even machines to compute the prime factorizations of larger numbers in 2009, scientists concluded a project using hundreds of machines to factor the 232-digit number, RSA-768, and it took two years. Thus, it can be seen that the prime factorization of 820, in either case, again is: The example below demonstrates two ways that a factor tree can be created using the number 820: In the example below, the prime factors are found by dividing 820 by a prime factor, 2, then continuing to divide the result until all factors are prime. Creating a factor tree involves breaking up the composite number into factors of the composite number, until all of the numbers are prime. This is essentially the "brute force" method for determining the prime factors of a number, and though 820 is a simple example, it can get far more tedious very quickly.Īnother common way to conduct prime factorization is referred to as prime decomposition, and can involve the use of a factor tree.

#Show me a list of prime numbers trial
Since 41 is a prime number, this concludes the trial division. Since 205 is no longer divisible by 2, test the next integers. As a simple example, below is the prime factorization of 820 using trial division: It involves testing each integer by dividing the composite number in question by the integer, and determining if, and how many times, the integer can divide the number evenly. Trial division is one of the more basic algorithms, though it is highly tedious. One method for finding the prime factors of a composite number is trial division. There are many factoring algorithms, some more complicated than others. Prime factorization is the decomposition of a composite number into a product of prime numbers.

As an example, the number 60 can be factored into a product of prime numbers as follows:Īs can be seen from the example above, there are no composite numbers in the factorization. This theorem states that natural numbers greater than 1 are either prime, or can be factored as a product of prime numbers. Prime numbers are widely used in number theory due to the fundamental theorem of arithmetic. Examples of this include numbers like, 4, 6, 9, etc. Numbers that can be formed with two other natural numbers, that are greater than 1, are called composite numbers. An example of a prime number is 7, since it can only be formed by multiplying the numbers 1 and 7. Prime numbers are natural numbers (positive whole numbers that sometimes include 0 in certain definitions) that are greater than 1, that cannot be formed by multiplying two smaller numbers. Related Factor Calculator | Common Factor Calculator


 0 kommentar(er)
0 kommentar(er)
